Degree Days.net Baseline Regression Tool

Regression is at the core of most analysis of heating/cooling energy consumption. A baseline regression describes energy consumption over a chosen baseline period, and is typically used to compare later energy consumption against baseline levels (e.g. to track ongoing performance or prove savings from changes made after the baseline period).

The regression tool tests thousands of regressions against your energy-usage data to help you choose the best regression (with the best HDD/CDD base temperatures) to represent baseline energy consumption.

You choose a weather station and copy/paste in your energy-usage data from a spreadsheet.
Degree Days.net generates HDD and CDD in a wide range of base temperatures and uses them to test thousands of regressions against your energy-usage data.
You download a spreadsheet of the regressions that give the best statistical fit, together with a range of statistics to help you assess their quality.
You choose the best regression (usually the first listed) and use it as the baseline for future analysis.

To use the regression tool: go to the Degree Days.net web tool and select "Regression" as the "Data type". Or continue reading this page to find out more about the regression tool and how best to use it.

Why use the regression tool instead of Excel?

A simple regression of energy consumption against heating degree days or cooling degree days is easy enough to do in Excel. But the Degree Days.net regression tool offers a lot more:

It does weighted regression, recommended by ASHRAE and others for improved accuracy, but difficult to do in Excel.
It does multiple regression against HDD and CDD together as well as single regression against HDD and CDD individually. This is important for buildings with both heating and cooling.
It tests thousands of regressions with different HDD and CDD base temperatures to find the ones that give the best statistical fit. For years we've recommended a similar process for single regression (either HDD or CDD alone), but we do not know of a realistic way to do this for multiple regression (HDD and CDD together) in Excel.
It automatically generates powerful extra statistics that can't all be easily calculated in Excel. For example, it generates the CVRMSE statistic that ASHRAE recommends, and, as well as R-squared, it generates the more sophisticated cross-validated R-squared which is better for assessing the predictive power of an energy model.

Copy/pasting in your energy data

The regression tool takes your energy-usage data and runs regressions against it. You will presumably have your energy data in a spreadsheet – you just have to check (and maybe modify) the format and then copy/paste the relevant data into the regression tool.

Step by step instructions for copy/pasting in your energy data

Select the relevant data in your spreadsheet (see the 2 allowed formats below), and hit Ctrl-c to copy it into the clipboard (Command-c on Mac).
Go back to the regression tool, click your mouse in the box, and hit Ctrl-v to paste (Command-v on Mac).
The regression tool should show you a table of your data... Check it over to see that it interpreted everything correctly. If it didn't, edit the data in your spreadsheet and try copy/pasting again.

Don't worry if your spreadsheet contains a lot of other analysis too – you can select/copy/paste only the cells that the regression tool needs.

Getting your spreadsheet data into the right format

Your energy data can have one of two formats. The examples below show the same data specified in each of the 2 formats:

The first-day-only format is a common format for spreadsheets of energy-usage data. The specified dates must be the first day of each period of measured energy usage. The last day of each period is assumed to be the day before the first day of the next. You may need extra rows with dates to specify any gaps in the data and to help the regression tool figure out when the last period ends:

First-day-only format (extra rows for gaps and at the end)

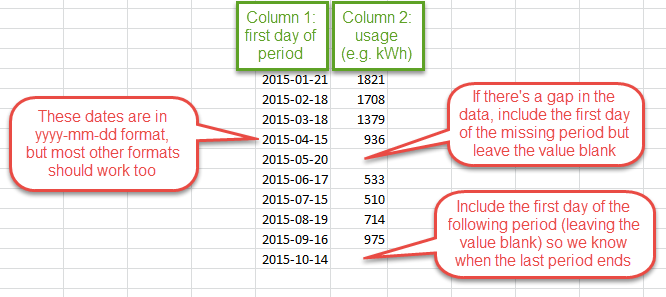
If your data is regular daily, weekly, monthly (each month starting on the same day), or yearly data, you shouldn't need the final row as the regression tool should figure out the end of the last period automatically. But it's not a bad idea to include it anyway, for clarity.

The first-and-last-day format can be a good one to use if you have gaps in your data as you can typically add an extra column (column 2 in the example below) and insert a few dates without affecting other parts of your spreadsheet:

First-and-last-day format (last day only needed for periods before a gap and at the end)

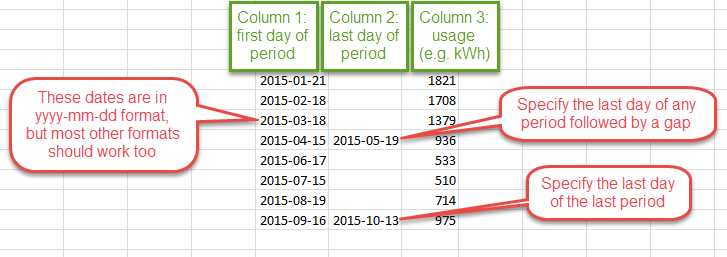
With the first-and-last-day format you can specify the last day of every period (in column 2), but for the normal case (the last day of one period being the day before the first day of the next) you can just leave it blank.

Date formats

Date formats are a source of much confusion for computer systems. Something like 10/11/12 is highly ambiguous as it can be interpreted as mm/dd/yy, or dd/mm/yy, or even yy/mm/dd.

We like the ISO date format yyyy-mm-dd because it is totally unambiguous. But we've programmed the regression tool to do its best to make sense of a variety of other formats as well. People from all over the world use Degree Days.net and we don't want to force them to change their spreadsheets any more than necessary before copy/pasting their data in.

So we suggest you try copy/pasting your data as it is. Our system will say if it can't make sense of it, and, if it interprets your dates wrong, you should be able to see from the table it displays immediately after you paste your data into the box.

If it's not working correctly, try changing the format of all your dates to yyyy-mm-dd. This is easy to do in Excel: select all the date cells, right-click, select "Format Cells...", then "Custom", type yyyy-mm-dd in the "Type:" box, and click "OK". If your original date format was a common one that you would expect to work automatically, please email us so we can see if there's a way we can improve the system.

Any units are fine for the energy-usage data

Energy-usage data would typically be in kWh, but other units like Btu, therms, litres, or gallons, are fine too. The regression tool does not know or care what the units are – it just processes the usage figures as numbers and gives you regressions that use whatever units you used in your copy/pasted input data.

Extra predictors (for Degree Days.net Pro customers)

With Degree Days.net Pro you can optionally include up to two extra predictors, like occupancy or production figures, in your regression analysis. Include them in additional columns to the right of your energy-usage data.

How to include extra predictors in your regression data (the c+ code is explained below)

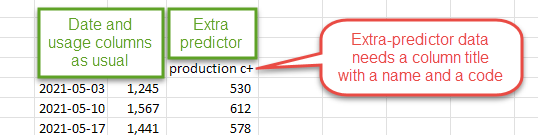
You will need to give your extra-predictor data column titles in a specific format that lets the regression tool know what they are called and how to process them. Titles should include a name and a code, like "production c+" in the example screenshot above. The code can be any of the following:

c+ for cumulative figures expecting a positive correlation with energy usage;
c- for cumulative figures expecting a negative correlation with energy usage;
c+- for cumulative figures expecting either a positive or negative correlation with energy usage;
a+ for average figures expecting a positive correlation with energy usage;
a- for average figures expecting a negative correlation with energy usage;
a+- for average figures expecting either a positive or negative correlation with energy usage.

Cumulative in this case means that the figures increase with time and so would typically be larger for longer periods (like a month) than for shorter periods (like a day). For example: total staff hours worked, total widgets produced.

Average in this case means that the figures are averaged (or normalized) in such a way that the length of the period does not affect them. For example: average number of rooms occupied (in a hotel), average widgets produced per hour.

A positive correlation means that larger extra-predictor figures are expected to lead to greater energy usage.

A negative correlation means that larger extra-predictor figures are expected to lead to lower energy usage.

A positive or negative correlation indicates that you don't know whether to expect the extra predictor to increase or decrease energy usage. It's usually best to avoid using this option, as usually it's best to figure out exactly what you expect from any extra predictors you include.

A word of caution about extra predictors

An extra predictor should only be included if it is an independent variable (i.e. not influenced significantly by another extra predictor or by degree days). R-squared will always increase (or at least never decrease) with the addition of any extra predictor (even a completely irrelevant one), but this is a quirk of statistics rather than an indication of a better model.

In some cases it may be better to use extra-predictor data to split your energy data into multiple sets, then run each set separately through the regression tool. For example, rather than using occupancy data as an extra predictor, you may be able to use it to split your energy data into occupied and unoccupied sets, getting a separate regression model for each. This way the regression tool will have the opportunity to use different base temperatures for each.

That said, there are certainly instances where it makes perfect sense to use extra predictors in a regression model, so don't be afraid to try them out! The regression tool will always test regressions both with and without any extra-predictor data you provide, so the stats can help you decide whether to use them or not.

Day normalization

If in doubt, just choose "Weighted", as it works well in all cases. Or read on for more information.

Day normalization is important for dealing with energy-usage data that has periods of different length (such as monthly data). The regression equations below show the key difference between regressions that are day normalized and regressions that aren't:

Regression equations

With day normalization (weighted or unweighted):

E = b*days + h*HDD 
E = b*days + c*CDD
E = b*days + h*HDD + c*CDD

Without day normalization:

E = b + h*HDD
E = b + c*CDD
E = b + h*HDD + c*CDD

Where:

E is the energy usage over the period in question;
days is the length (in days) of the period in question;
HDD is the heating degree days over the period in question;
CDD is the cooling degree days over the period in question;
b, h, and c are regression coefficients (the regression tool calculates these).

Day-normalized regression equations require you to plug in the length (in days) of the period that you want to calculate baseline-predicted energy consumption for. In contrast, regressions that aren't day normalized only work for periods of the same length as the periods in the original baseline data – that period length is effectively built into the baseload coefficient (b) already.

If your baseline data (what the regressions are calculated from) has periods that are all the same length (e.g. daily or weekly data), day normalization is not important. With such data, regression with weighted and unweighted day normalization will give the same results, and regression with no day normalization will give a baseload coefficient (b) that is simply the period length (in days) multiplied by the baseload coefficient given by day-normalized regression. The other coefficients (h and c) will be the same as those given by day-normalized regression.

However, day normalization is important for regressions from data with periods of different length, as it will improve the accuracy of the coefficients. The more variation there is in the period lengths, the more difference there will be in the calculated coefficients.

In summary:

Weighted day normalization is the recommended option. It gives the best results for data with periods of different length, and the weighting makes no difference if the periods are all the same length. Longer periods effectively have a greater influence on the regression coefficients than shorter periods. The only real downside of weighted day-normalization is that it is very difficult to replicate in Excel. But, with our regression tool to run the regressions for you, that shouldn't be a problem. You don't need to actually run the regressions in Excel to be able to use the regression equations that the regression tool gives you in Excel.
Unweighted day normalization – for data with periods of different length this is typically better than using no day-normalization at all, but it's not as good as the weighted option. It is, however, easy to replicate in Excel by regressing energy usage per day against degree days per day.
None – no day normalization at all. This works fine for data with periods that are all the same length, but not so well for data with periods of different length. We've included it as an option because, despite its inaccuracies, it is widely used, and it is easy to replicate in Excel (just regress energy usage against degree days).

Note that monthly data typically has periods of different length (as calendar months can be 28, 29, 30, or 31 days in length), so it's definitely best to use day normalization (and preferably weighted day normalization) when running regressions against it. For consistency of your post-regression calculation processes we recommend using day normalization (and preferably weighted day normalization) for all the data you work with, whether it has different-length periods or not.

Specifying base temperatures to include in the results

The "Include in results" option lets you specify a heating base temperature and a cooling base temperature for which regressions will be included in the results along with the auto-selected ones.

As the regression tool tests thousands of base-temperature combinations automatically, your chosen base temperatures will probably be tested whether you specify them or not. But by specifying them here you can see how their regressions compare with those in the auto-selected shortlist. If the statistics are close, you might want to use them instead of the auto-selected ones.

If you don't have a good idea of the base temperature(s) you want, you can just leave them on the default values to see how much better it is to choose optimal base temperatures than to stick with historically-prescribed defaults like 15.5°C or 65°F.

Interpreting the results

After testing thousands of regressions against your energy-usage data, the Degree Days.net regression tool returns a spreadsheet with details of the regression(s) that gave the best statistical fit (the "shortlist"), and any others that were notable (e.g. for data that looks like it was from a heating-only building the regression tool will typically also return the best CDD-only regression, even though it's unlikely to make it into the shortlist).

The spreadsheet output contains the following columns of data:

Regression – the ranking of each regression. The system aims to list the regressions in best-to-worst order, and it labels the likely candidates with "shortlist". Typically you'll want to use the first-listed regression from the shortlist. But, with knowledge of the building, you may decide that another regression is a better choice. For example, if you know that the building has heating but no cooling, you may want to choose a regression with HDD but no CDD, even if it's not the first listed, and occasionally even if it's not in the shortlist. Though do watch out for regressions with negative coefficients (see below).
Equation – the regression equation into which you would plug the relevant coefficients from the other columns. This enables you to quickly see which parameters are relevant for each regression listed, and it highlights the way in which you can use each regression to calculate baseline-predicted energy usage over any period for which you have degree days in the base temperature(s) specified by the regression.
Station ID – the ID of the weather station that was used to generate the degree days that your energy-usage data was regressed against.
Readings – (a.k.a. sample size or sample count) the number of energy-usage-data readings that were used for the regression. If this is less than the number of readings you copy/pasted in it's because the weather station you selected did not have enough recorded temperature data to generate degree days matching all of your energy-usage periods.
First day – the first day of the first energy-usage period that was used for the regression. You can check this against the first day of your original energy-usage data – if they're not the same you might want to try again with another weather station, as presumably the weather station you selected did not have enough recorded temperature data to generate degree days to match all your energy-usage data.
Last day – the last day of the last energy-usage period that was used for the regression.
Total days – the number of days covered by the energy-usage data that was used for the regression. If there were no gaps in the usage data this will simply be the number of days between the first day and the last day.
Gap days – the number of days between the first day and the last day for which there was no energy-usage data. Degree days from Degree Days.net are always continuous (no gaps), so, if this number is greater than zero, it will be because of gaps in your original energy-usage data rather than gaps in the degree days generated to match it.
DD % est – the "% estimated" figure associated with the degree days that were used for the regression – a number between 0 and 100 indicating the extent to which the degree days were based on estimated temperature data used to fill in missing or erroneous temperature readings from the weather station you selected.
HDD base (C or F) – the heating base temperature of the regression. To use the regression equation you'd want to download HDD in this base temperature. This will be blank if the regression did not include HDD.
CDD base (C or F) – the cooling base temperature of the regression. To use the regression equation you'd want to download CDD in this base temperature. This will be blank if the regression did not include CDD.
HDD total – the total heating degree days (in the HDD base temperature) over the period covered by the energy-usage data used for the regression (excluding gaps). This will be blank if the regression did not include HDD.
CDD total – the total cooling degree days (in the CDD base temperature) over the period covered by the energy-usage data used for the regression (excluding gaps). This will be blank if the regression did not include CDD.
Baseload (b) – the baseload coefficient in the regression equation (e.g. the b in E = b*days + h*HDD + c*CDD). Watch out for negative values (see below). For day-normalized regressions (which we recommend) you'll want to multiply this by the number of days covered by the period you're considering (the period that you want the baseline-regression-predicted energy consumption for and the period that your HDD/CDD values cover).
HDD coef (h) – the HDD coefficient in the regression equation (e.g. the h in E = b*days + h*HDD). Watch out for negative values (see below).
CDD coef (c) – the CDD coefficient in the regression equation (e.g. the c in E = b*days + c*CDD). Watch out for negative values (see below).
R2 – the R-squared value for the regression. This is the same R-squared that you will be familiar with if you have run regressions in Excel (or added a linear trend line to a scatter plot). Higher values are better, but be careful: R-squared favours more complicated regression models, so it's not great for comparing different types of energy regressions (like comparing an HDD+CDD regression with an HDD-only or CDD-only regression). For more on this see the notes for adjusted R-squared below.
R2 adjusted (adjusted R-squared) – like R-squared, but adjusted downwards to account for the number of predictors (like e.g. HDD and CDD) in the regression equation. To some extent this corrects for the fact that R-squared will always increase (or at least never decrease) if you add more predictors into a regression, so it is better than R-squared if you're comparing, say, a regression of energy against HDD alone with a regression of energy against both HDD and CDD. It's a standard statistical measure (not specific to energy or degree days) that you will find plenty more information about online if you search. However, cross-validated R-squared is typically a more useful statistic for baseline energy regressions.
R2 cross-validated (cross-validated R-squared or predicted R-squared) – like R-squared but calculated in a more sophisticated way. Whilst R-squared only gives an indication of how good the regression is at explaining the sample usage data it was generated from, cross-validated R-squared gives an indication of how good the regression is likely to be at predicting energy consumption (according to baseline levels) in the future. It's calculated using a process called leave-one-out cross-validation. It's a standard statistical measure (rather than being specific to the energy field), and you can find more information about it online if you search for "cross-validated R-squared" or "predicted R-squared". It's derived from the PRESS statistic which you can also look up. But you don't need to understand cross-validated R-squared fully to know that it is essentially a more-sophisticated R-squared that is in many ways better for choosing regressions and assessing the quality of a baseline energy model. Like R-squared it has a value of 1 or less (1 being the best value), and it is typically greater than zero, though, unlike R-squared, it can be negative for really bad regressions. Also, unlike R-squared, it doesn't have the problem of consistently favouring more complicated regression models.
S – the standard error of the regression. This is a common statistic (not energy-specific) that you can look up online. It will always be zero or greater, and lower values are better. You can think of it as a ± value on the E values calculated by the regression, though, like R-squared, adjusted R-squared, and CVRMSE, it is only an indication of the regression's ability to explain the sample energy-usage data that it was generated from – it's not like cross-validated R-squared which indicates the ability of the regression to predict energy consumption from HDD/CDD values that didn't feed into the original model (i.e. from outside the baseline period).
CVRMSE (Coefficient of Variation of the Root Mean Square Error) – a statistic recommended by ASHRAE (e.g. in their often-referenced Guideline 14) to assess the quality of a baseline regression. Lower values are better. For calculation of savings compared to a baseline model ASHRAE likes to see a baseline regression with CVRMSE below 0.25 if there is at least 12 months' worth of post-baseline consumption data to be compared with the baseline-predicted consumption, or below 0.2 if there is less than 12 months' worth. You will often see CVRMSE expressed as a percentage (e.g. 0.2 expressed as 20%) – to turn the spreadsheet figures into percentages just multiply them by 100. Note that CVRMSE does not penalize regressions with more predictors, nor does it involve any cross-validation, so we don't recommend using it over cross-validated R-squared to choose between the regressions returned by the regression tool. It's a useful statistic, but that's not what it's built for.
Baseload S – the standard error of the baseload coefficient. This is a measure of the precision of the regression model's estimate of the baseload coefficient value. It's a common statistic (not energy specific) that you can look up online.
Baseload P – the p-value of the baseload coefficient. See the explanation of HDD coef P below. The p-value for the baseload coefficient is usually high if the baseload coefficient is small, so it's often not as useful as the other p-values when assessing the quality of a regression.
HDD coef S – the standard error of the HDD coefficient. This is a measure of the precision of the regression model's estimate of the HDD coefficient value. It's a common statistic (not energy specific) that you can look up online.
HDD coef P – the p-value of the HDD coefficient. It can have values between 0 (best) and 1 (worst), and you can use it as an indication of whether there is likely to be a meaningful relationship between HDD and energy consumption. People often look for p-values of 0.05 or less, but really it is a sliding scale. p-value is a common statistic (not energy specific) that you can look up online.
CDD coef S – the standard error of the CDD coefficient. See the explanation of HDD coef S above.
CDD coef P – the p-value of the CDD coefficient. See the explanation of HDD coef P above.

Watch out for negative coefficients!

A negative coefficient (on the baseload, HDD, or CDD) is usually an indication that the regression is not a good one. A regression with one or more negative coefficients can often look good in other respects (i.e. good statistics), but it is unlikely to be justifiable in real-world terms, so is typically best ignored.

For informational purposes the regression tool will return regressions with negative coefficients if they fit better than any other regressions with the same equation (e.g. E = b*days + h*HDD, E = b*days + c*CDD, or E = b*days + h*HDD + c*CDD), but it will always list them below any regressions with only non-negative coefficients.

Choosing the best regression

The regression tool has a sophisticated process for comparing and ranking the thousands of regressions that it tests against each set of energy-usage data. The shortlist regressions are the ones it considers to be likely candidates, and the first-listed regression is the one it thinks best. But the regression tool knows nothing about the building that your energy-usage data came from. And, although we are always looking to improve the regression tool's algorithms, it is based on statistics and probabilities so it will never be possible for it to be correct 100% of the time.

If a building has no cooling then you're unlikely to want a regression involving CDD, even if the first-listed regression involves CDD. For a building with no heating you're unlikely to want a regression involving HDD. (Although if the numbers for such surprise regressions look much better than they do for the others it may be worth you questioning your assumptions about the building and the equipment that your metered energy is feeding.)

An experienced energy professional will often have a rough idea of the likely base temperature(s) of a building, the likely baseload energy consumption (expressed in the baseload coefficient of the regression equation), and the likely split of energy usage between baseload, heating, and cooling, over the baseline period of energy-usage data provided. This knowledge can help further in choosing the best regression.

If you have good knowledge of the building, use it!

Favour regressions with the predictors you expect (e.g. HDD only, CDD only, HDD and CDD together).
Favour regressions with base temperatures that you can justify in terms of the building and its operation (our article on estimating base temperatures should help).
Look at the regression coefficients and the HDD total and CDD total figures to see how much energy usage each regression attributes to heating, cooling, and baseload (non-weather-dependent consumption accounted for by the baseload coefficient), over the baseline period your energy-usage data covers. Favour regressions with usage breakdowns that fit with your expectations.

Though do check the statistics before choosing any regression that isn't in the shortlist. Here are some tips on comparing regressions based on the statistics:

Watch out for negative coefficients (see above). A regression with one or more negative coefficients (including a negative baseload coefficient) is unlikely to be a good one.
Cross-validated R-squared is a particularly useful statistic for comparing regressions that were generated from the same energy-usage data. It gives an indication of the power of a regression to predict future energy consumption according to baseline levels (the main purpose of baseline regressions), whilst R-squared, adjusted R-squared, the standard error (S), and CVRMSE are only measures of how well a regression explains the energy-usage data that it was generated from. Predictive power versus explanatory power is an often-discussed topic in statistics, and the two often go hand in hand, but the key things to remember are that prediction is typically more important for energy regressions, and that cross-validated R-squared is a useful measure of a regression's predictive power (and one that is highly intuitive thanks to its similarity to the familiar R-squared).
The p-values of the HDD and CDD regression coefficients (HDD coef P and CDD coef P) can be useful. A high p-value is an indication that the predictor might not belong. For example, if a regression with HDD and CDD has a high p-value for the CDD coefficient, it is an indication that perhaps an HDD-only regression would be better. The p-value of the baseload coefficient isn't typically so useful, however, because it's usually high when the baseload is small (which it often rightfully is).

Bear in mind that the regression tool already aims to use the statistics as best it can when choosing and ranking the regressions it returns from the thousands it tests against each set of energy-usage data. It will always be possible to improve the algorithms, but it should be doing a pretty good job. However, a statistics-only approach can only go so far, and, with knowledge of the building, you will often find that regression 2 or below will be a better choice than the one the regression tool put first.

Help us improve the regression tool

Please email us at info@degreedays.net with any feedback about the regression tool. We'd love to hear what you like about it, what you don't like about it, and what else it could do to make it more useful to you.

About sending us data...

For quite a while after we launched the regression tool in beta in October 2015 we were particularly keen for people to send us real-world energy-usage data with which we could test and improve the regression-tool's algorithms. We have now received a lot of data to work with (thank you!) and getting more is no longer a priority for us. But if you do have an interesting data set that you would like to discuss, or that highlights a good or bad aspect of the regression tool, please do send it along, together with the following information:

The fuel that the energy data represents (e.g. gas or electricity).
The location of the building that it came from (so we can choose one or more weather stations to test the data against).
Whether the building has heating, or cooling, or both.
What other fuels supply the building.
Which fuel(s) supply which components of the heating/cooling system (e.g. gas heating, electric cooling).
What temperature the building is heated/cooled to (these are often different).
Whether it is heated/cooled 24/7 or intermittently (e.g. for office hours only).
Whether it is well insulated.
Whether it has any significant internal heat gains (e.g. equipment that generates a lot of heat).
Whether it has any significant refrigeration or freezer loads.
Anything else that you think is likely to be relevant.

Sorry about the long list, it's just that we need to know about the building and its usage to figure out whether or not the regression tool is giving useful results for any given set of data.

Thank you!